How to Draw Moment Diagram From Shear Diagram

March 06, 2022 Post a Comment

Chapter 6: Internal Forces

6.2 Shear/Moment Diagrams

Shear/Moment diagrams are graphical representations of the internal shear force and bending moment along the whole beam.

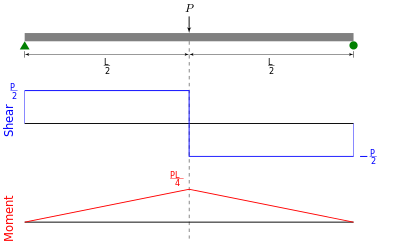
Source (image): By XFEM Skier – Own work, CC By-SA 3.0, https://commons.wikimedia.org/w/alphabetize.php?curid=29178249

Shearing Strength Diagram

This is a graphical representation of the variation of the shearing force on a portion or the entire length of a beam or frame. As a convention, the shearing force diagram can be fatigued above or below thex-centroidal axis of the structure, merely it must exist indicated if information technology is a positive or negative shear force.

Bending Moment Diagram

This is a graphical representation of the variation of the bending moment on a segment or the entire length of a beam or frame. Every bit a convention, the positive angle moments are drawn above thex-centroidal centrality of the structure, while the negative bending moments are drawn below the axis.

Below is a simple case of what shear and moment diagrams look like, afterwards, the relation between the load on the beam and the diagrams volition be discussed.

Source: Internal Forces in Beams and Frames, LibreTexts. https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/i.04%3A_Internal_Forces_in_Beams_and_Frames

There is a relationship betwixt distributed loads and shear/moment diagrams. Simply put:

[latex]\frac{dM}{dx}=5(x)[/latex]

[latex]\frac{dV}{dx}=-westward(ten)[/latex]

[latex]\frac{d^2M}{dx^2}=-w(x)[/latex]

Or:

[latex]\Delta Grand=\int Five(x)dx[/latex]

[latex]\Delta 5=\int west(x)dx[/latex]

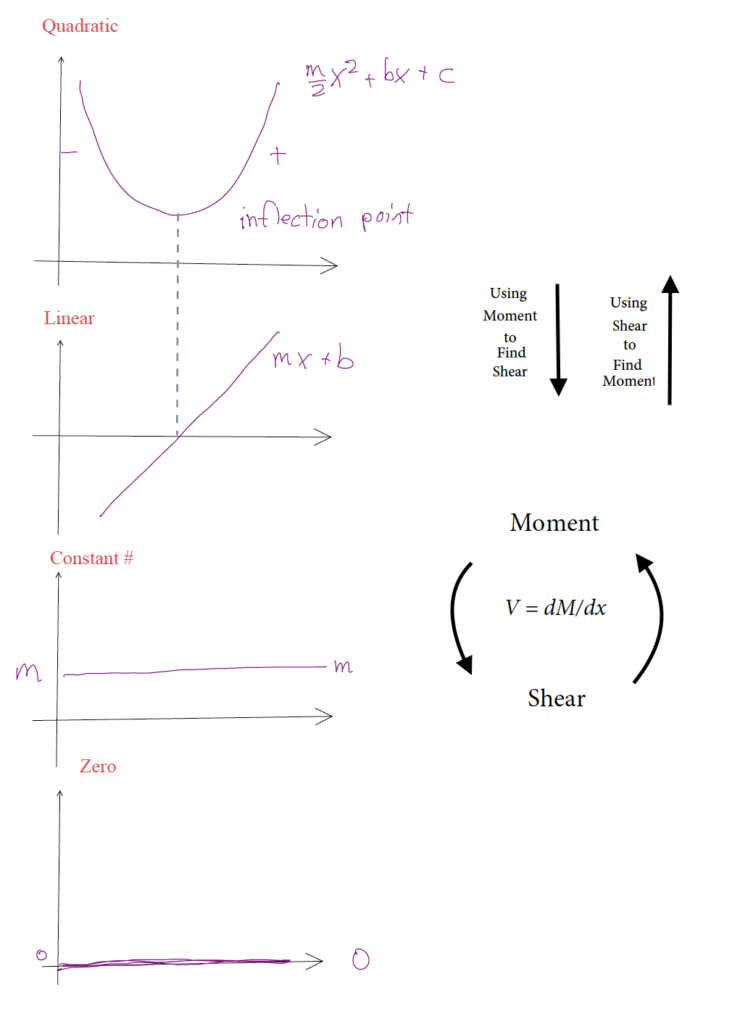
So, if at that place is a constant distributed load, so the slope of shear will be linear and the gradient of the moment will be parabolic. If distributed load is 0, so the shear will be constant and the slope of the moment will exist linear (every bit shown in instance i in the next section).

For the derivation of the relations amongw, V, andM, consider a simply supported axle subjected to a uniformly distributed load throughout its length, equally shown in the effigy below. Let the shear strength and bending moment at a department located at a distance ofx from the left support beV andGrand, respectively, and at a sectionx +dx beV +dV andM +dM, respectively. The full load interim through the center of the infinitesimal length iswdx.

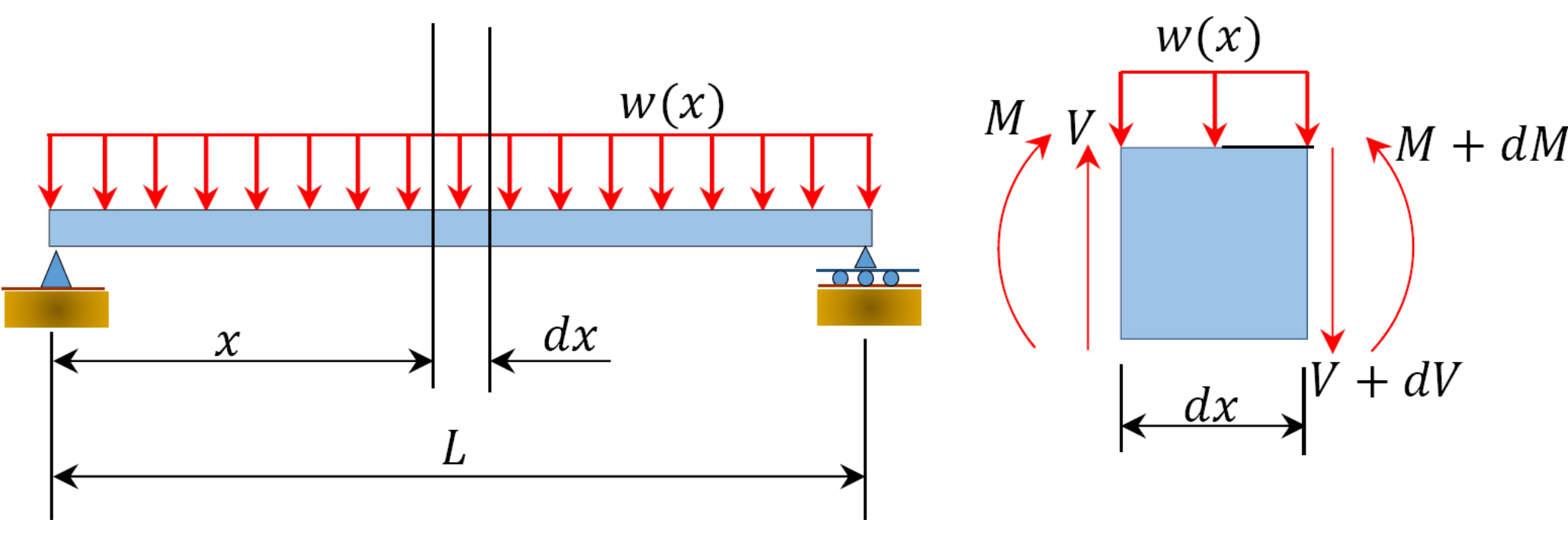
To compute the bending moment at section x + dx, use the following:

[latex]M_{ten+dx}=Grand+Vdx-wdx \cdot dx/two\\ \qquad \quad=G+Vdx \text{ (neglecting the pocket-size 2nd order term wdx^2/2)}[/latex]

[latex]G+dM=M+Vdx[/latex]

[latex]\frac{dM}{dx}=V(x)[/latex] (Equation 6.1)

Equation 6.ane implies that the outset derivative of the angle moment with respect to the distance is equal to the shearing force. The equation as well suggests that the gradient of the moment diagram at a particular signal is equal to the shear force at that aforementioned betoken. Equation 6.1 suggests the following expression:

[latex]\Delta M=\int Five(x)dx[/latex] (Equation vi.2)

Equation six.2 states that the modify in moment equals the surface area nether the shear diagram. Similarly, the shearing strength at section10 +dx is every bit follows:

[latex]V_{ten+dx}=5-wdx\\V+dV=5-wdx[/latex]

[latex]\frac{dV}{dx}=-w(x)[/latex] (Equation vi.3)

Equation vi.3 implies that the first derivative of the shearing force with respect to the distance is equal to the intensity of the distributed load. Equation 6.three suggests the post-obit expression:

[latex]\Delta 5=\int w(x)dx[/latex] (Equation six.4)

Equation 6.4 states that the change in the shear force is equal to the expanse under the load diagram. Equation 6.ane and half dozen.iii suggest the following:

[latex]\frac{d^2M}{dx^2}=-westward(x)[/latex] (Equation 6.5)

Equation 6.5 implies that the 2nd derivative of the angle moment with respect to the altitude is equal to the intensity of the distributed load.

There are many methods yous can use to solve a shear/moment diagram. First, you can find the equation for each portion and integrate using the above equations.

Second, you lot could use the method shown in the previous department to calculate the internal forces at important points (where loads are applied, the start and cease of distributed loads, at reaction points). Plot these points on the V and Thou plots at the x locations, and then connect the dots using the advisable shape slope (more on this at the bottom of this folio).

Third, you can find the equations by using the equilibrium equations (and so there'due south no integration/differentiation).

Adjusted from original source https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/ane.04%3A_Internal_Forces_in_Beams_and_Frames

Depict a FBD of the structure
Calculate the reactions using the equilibrium equations (may not need to do this if choosing a cantilever beam and using the complimentary side for the FBD).
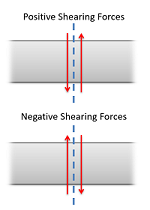
Make a cut and add internal forces Due north V and M using the positive sign convention. Depending on the number of loads, you may need multiple cuts. Call up the positive convention:
For shear, find an equation (expression) of the shear that is x altitude from the origin (oftentimes the reaction) for each cut.
For moment, find an equation (expression) of the shear that is x distance from the origin (often the reaction) for each cutting.
Plot these equations on a plot on top of each other.

The rest of this section will apply this method.

Case 1

(adapted from https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/one.04%3A_Internal_Forces_in_Beams_and_Frames)

Draw the shear force and bending moment diagrams for the cantilever axle supporting a full-bodied load of 5 lb at the free end three ft from the wall.

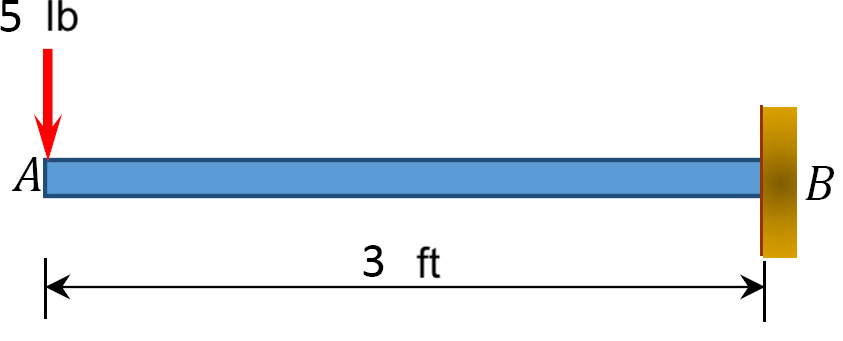
1. Draw a FBD of the structure

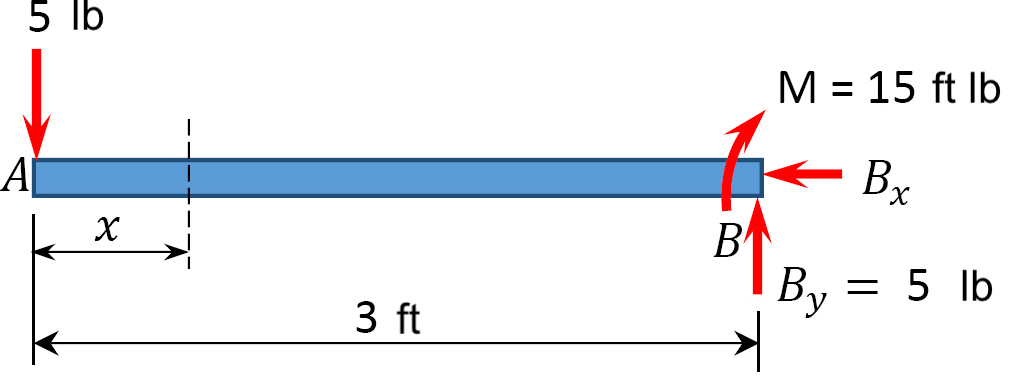
two. Calculate the reactions using the equilibrium equations (may not need to do this if choosing a cantilever beam and using the free side for the FBD).

First, compute the reactions at the support. Since the support at B is stock-still, at that place will exist 3 reactions at that support, namely B_y , B₁₀ , and M_B . Applying the conditions of equilibrium suggests the following:

[latex]\sum F_{x}=0: \quad \underline{B_{x}=0}[/latex]

[latex]\sum F_{y}=0: \quad-v lb+B_{y}=0[/latex]
[latex]\qquad \quad \underline{B_{y}=5 lb}[/latex]

[latex]\sum M_{B}=0: \quad(5 lb )(3 \mathrm{ft})-M=0[/latex]
[latex]\qquad \quad \underline{M=15 ft \cdot lb}[/latex]

three. Make a cut and add internal forces N V and Thou using the positive sign convention. Depending on the number of loads, y'all may need multiple cuts

Only 1 cut needed because only i load is added at the end. (If it were in the centre there would be 2 sections to consider). The value x could exist 0 to three ft.

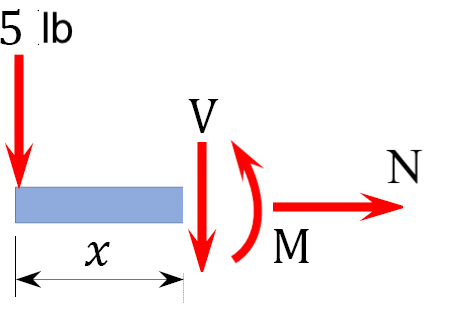
4. For shear, find an equation (expression) of the shear that is x distance from the origin (often the reaction) for each cut.

ten is the distance from the free end of the cantilever axle to the cut. The shearing force at that department is due to the applied load. Using the equilibrium equations,

[latex]\sum F_y = -5 lb - 5 = 0 \\ \qquad \quad \underline{Five = - v lb} \text{ (- indicates V acts in opposite direction)}[/latex]

The constant number for shear means that information technology doesn't modify or vary by x. (If there were a distributed load, ten would be function of the equation).

The negative sign indicates the shear actually goes the opposite direction. (This is due to the fact that the sign convention for a shearing force states that a downward transverse force on the left of the section under consideration volition cause a negative shearing force on that department.)

5. For the moment, notice an equation (expression) of the shear that is ten distance from the origin (often the reaction) for each cutting.

Here, x is measured from the left. Using sum of the moments equations, find an expression for Yard. You lot could choose to sum the moments about the end signal where the load is applied, or y'all could do it at the moving indicate x. Both take the aforementioned endeavour for this problem, so let's cull the left hand side where the five lb are being applied.

[latex]\sum M_L = -Vx - M = 0[/latex]

[latex]\qquad \quad M = + Vx = (-5 lb) * x[/latex]

[latex]\qquad \quad \underline{M = -(5lb)x } \text{ (the negative sign indicates the pointer goes the other management.}[/latex]

The obtained expression is valid for the unabridged beam (the region 0 < x < iii ft). The negative sign indicates a negative moment, which was established from the sign convention for the moment, and then the moment actually goes in the reverse management. The moment due to the 5 lb strength tends to cause the segment of the axle on the left side of the department to showroom a downward concavity, and that corresponds to a negative angle moment, according to the sign convention for angle moment.

6. Plot these equations on a plot on top of each other.

Note that because the shearing force is a constant, it must be of the same magnitude at whatever bespeak along the beam. As a convention, the shearing force diagram is plotted higher up or below a line corresponding to the neutral axis of the axle, merely a plus sign must be indicated if it is a positive shearing forcefulness, and a minus sign should be indicated if it is a negative shearing force. A manner to check the reply is to ensure the reaction force brings the problem back to 0. The shear is -5 until the terminal moment when the reaction strength of +5lb brings the force to 0.

Since the role for the bending moment is linear, the bending moment diagram is a straight line. Thus, it is enough to use the 2 principal values of bending moments determined at x = 0 ft and at ten = 3 ft to plot the bending moment diagram. Equally a convention, negative bending moment diagrams are plotted below the neutral centrality of the beam, while positive bending moment diagrams are plotted to a higher place the axis of the beam.

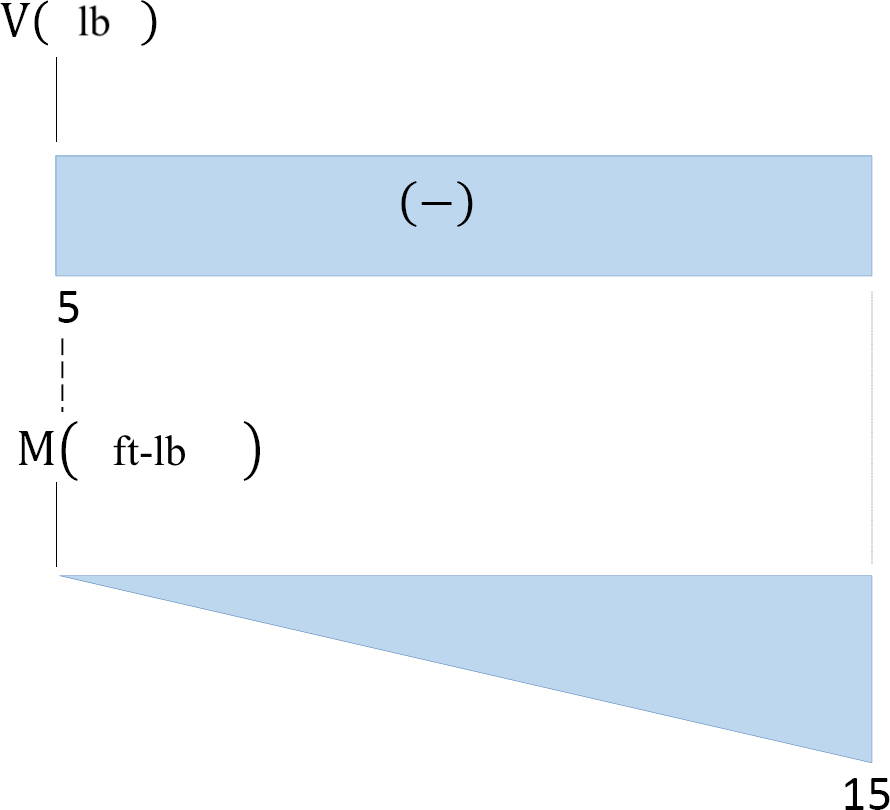
Notice the units are included in the axes.

Here is a second explanation for how to create shear/moment diagrams:

Shear Diagram

To create the shear force diagram, we will use the post-obit process.

Solve for all external forces interim on the torso.
Draw out a free trunk diagram of the body horizontally. Exit all distributed forces every bit distributed forces and exercise not replace them with the equivalent point load.
Lined up beneath the gratuitous body diagram, describe a gear up of axes. The x-axis will stand for the location (lined upwardly with the free torso diagram higher up), and the y-axis will represent the internal shear force.
Starting at zero at the right side of the plot, you volition motion to the right, pay attention to forces in the free body diagram to a higher place. As you lot move right in your plot, continue steady except…
- Leap upwards past the magnitude of the force for any point forces going up.
- Jump downwards by the magnitude of the force for any point forces going down.
- For any uniform distributed forces you will take a linear slope where the magnitude of the distributed force is the slope of the line (positive slopes for upwards distributed forces, negative slopes for downwards distributed forces).
- For non-uniform distributed forces, the shape of the shear diagram plot volition be the integral of the strength role.
- Y'all can ignore any moments or horizontal forces practical to the body.
By the time you lot get to the left end of the plot, you should always current of air up coming back to nix. If y'all don't wind up dorsum at zero, go back and cheque your previous work.

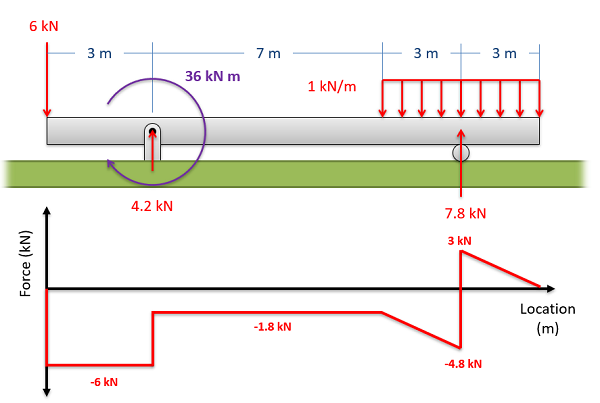
To read the plot, you simply need to find the location of interest from the free body diagram above, and read the corresponding value on the y-axis from your plot. Positive numbers correspond an upwards internal shearing force to the right of the cross section and a downwards strength on the left, and negative numbers betoken a downwards internal shearing force to the right of the cantankerous section and a upwards force on the left. A visual of these forces can be seen in the diagram to the right.

Moment Diagram

The moment diagram will plot out the internal bending moment within a horizontal beam that is subjected to multiple forces and moments perpendicular to the length of the beam. For practical purposes, this diagram is often used in the same circumstances as the shear diagram, and more often than not both diagrams will be created for analysis in these scenarios.

To create the moment diagram for a shaft, we will use the following process.

Solve for all external forces and moments, create a gratuitous body diagram, and create the shear diagram.
Lined upward below the shear diagram, draw a set of axes. The x-axis will stand for the location (lined upward with the shear diagram and free body diagram in a higher place), and the y-axis will represent the internal bending moment.
Starting at null at the right side of the plot, you volition motility to the right, pay attending to shear diagram and the moments in the free trunk diagram above. As yous move right in your plot, the moment diagram volition primarily exist the integral of the shear diagram, except…
- Spring upwards by the magnitude of the moment for whatsoever negative (clockwise) moments.
- Leap downwards by the magnitude of the moment for any positive (counter-clockwise) moments.
- You can ignore any forces in the free body diagram.
By the time you go to the left terminate of the plot, you should always wind up coming back to zero. If y'all don't current of air upwards dorsum at nothing, become back and check your previous piece of work.

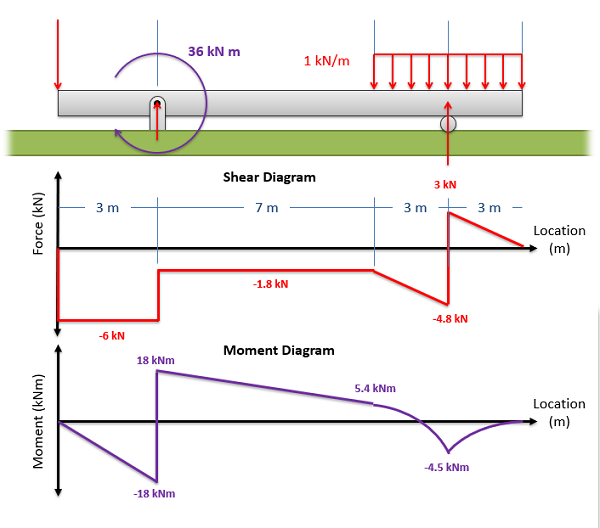
To read the plot, you lot merely need to take the find the location of interest from the free torso diagram to a higher place, and read the corresponding value on the y-axis from your plot. Positive internal moments would cause the beam to bow downward (remember a smile shape) negative internal moments will cause the beam to bow upwards (think a frown shape). You can as well run across the positive and negative internal moments in the effigy to the correct.

Source: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/6_internal_forces/six-4_shear_moment_diagrams/shear_moment_diagrams.html

Example 2

Draw the shearing force and angle moment diagrams for the cantilever beam subjected to a uniformly distributed load in its entire length, as shown in Figure four.5a.

Answer:

Support reactions.

First, compute the reactions at the back up. Since the back up at B is stock-still, there will possibly be three reactions at that support, namely B_y , B_ten , and M_B , as shown in the costless-trunk diagram in Figure 4.4b. Applying the atmospheric condition of equilibrium suggests the post-obit:

Shear Strength Function

Let x be the distance of an arbitrary section from the free end of the cantilever beam, as shown in Effigy 4.5b. The shearing strength of all the forces interim on the segment of the beam to the left of the section, as shown in Figure 4.5e, is determined every bit follows:

The obtained expression is valid for the entire beam. The negative sign indicates a negative shearing force, which was established from the sign convention for a shearing force. The expression also shows that the shearing force varies linearly with the length of the axle.

Shearing force diagram. Annotation that because the expression for the shearing force is linear, its diagram will consist of straight lines. The shearing force at x = 0 thou and x = v m were adamant and used for plotting the shearing force diagram, equally shown in Figure 4.5c. As shown in the diagram, the shearing force varies from zero at the free finish of the beam to 100 kN at the fixed end. The computed vertical reaction of B_y at the support tin exist regarded as a check for the accurateness of the analysis and diagram.

Angle Moment Function

The expression for the bending moment at a department of a distance 10 from the free end of the cantilever beam is equally follows:

The negative sign indicates a negative moment, which was established from the sign convention for moment. As seen in Effigy four.5f, the moment due to the distributed load tends to cause the segment of the beam on the left side of the section to exhibit an upward concavity, and that corresponds to a negative angle moment, according to the sign convention for bending moment.

Bending moment diagram. Since the office for the bending moment is parabolic, the angle moment diagram is a curve. In addition to the two principal values of bending moment at x = 0 m and at 10 = 5 m, the moments at other intermediate points should be determined to correctly draw the bending moment diagram. The bending moment diagram of the beam is shown in Figure 4.5d.

Source: Internal Forces in Beams and Frames, Libretexts. https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_Frames

The post-obit examples show the shear and moment diagrams for each beam. For details on how to solve each, get to: https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_Frames

Though there are exceptions, these rules are generally true:

+V means increasing K
-V means decreasing G
When V = 0, that'southward max or min M

How does each plot start/terminate? Reactions only if no applied load/moment at ends:

Cantilever:
- At start/reaction: Nonzero V and M
- At finish/unsupported end: 0 for both
Simply supported
- For V: Start and terminate with reaction forces
- For M: Start and end at zero
Where are the 'jumps' or inflection bespeak where lines alter?
- In V, forces 'jump' up or down where applied forces are, matching the direction they are applied (also reactions)
- In M, moments bound upwards or downwardly where applied moments are, matching the management
Relationship between graphs
- When at that place is in increasing slope in M, then Shear should exist positive
- When in that location is a decreasing slope in M, then Shear should be negative
- When V is positive, M should exist increasing
- When V is negative, M should be decreasing
- When intensity is positive, V should exist increasing
- When intensity is negative, V should be decreasing
- Inflection points in the M plot (where the slope of the line changes from negative to positive & max/min values) should be 0 in the V plot
- A aught value in the V plot should produce a max or min value in the M plot

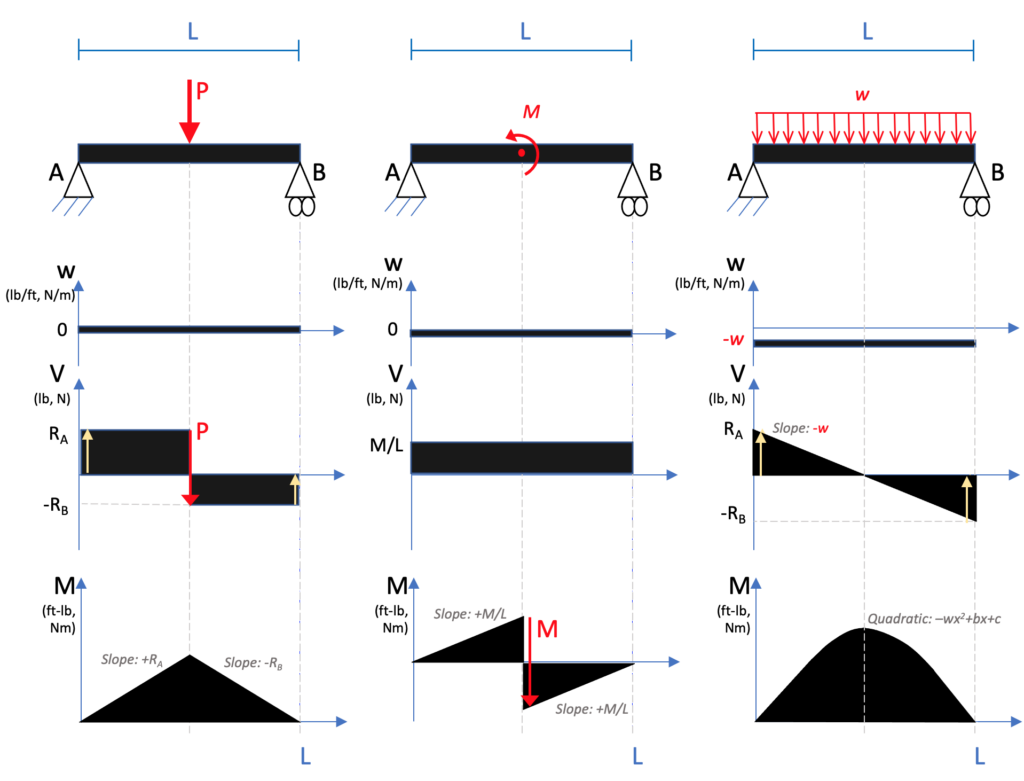
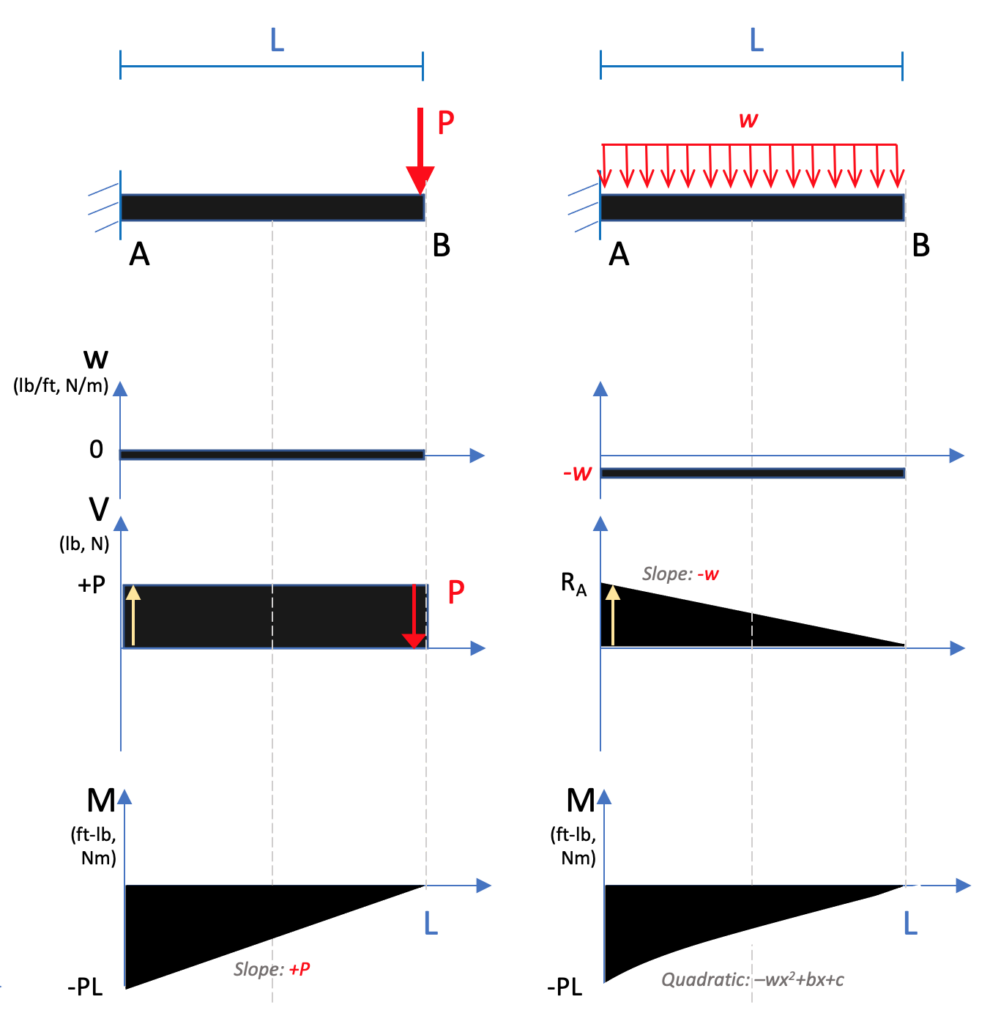
The following figure shows the relationship between the derivatives. Remember that the derivative of x2 (quadratic) = x (linear). The derivative of x (linear) is a constant number. The derivative of a constant number is 0. The derivative of moment is shear, and then if yous take the shape of the moment, employ this figure to judge the shape of shear by going down the plots.

The contrary is true when going from shear to moment. The integral of shear is moment. The integral of 0 is a constant number. The integral of a constant number is linear. The integral of linear is quadratic. (The integral of quadratic is cubic). This progression moves up the plots from the bottom to the top.

In that location are a few online programs that tin assist ostend the shape that y'all found or assistance you learn how to translate loads into shear and moment diagrams. These are non acceptable to use on the test or in homework and have express complimentary versions. This is not an endorsement of any of the sites, but showing learning tools.